There is always some water vapor in the air, and the pressure and temperature nearly always vary from theoretical. This means that correction factors based on physical elevation alone (such as NHRA's national record e.t./mph correction factors) don't cut it when it comes to estimating engine output or fuel-system calibration. Likewise, if the observed temperature is 42.2 degrees F, the barometer reads 24.9 in-Hg, and there is no humidity, the density altitude is about 5,000 feet, no matter the actual elevation. In other words, the actual physical altitude at your location may be 3,000 feet, but the air condition is exactly like a theoretically perfect day at 5,000 feet.
Effectively, this concept of density altitude gives us a snapshot of what the air is "really like" at our location, plus a tool by which to tune the car. On this slide you will find typical values of the properties of air at sea level static conditions for a standard day. We are all aware that pressure and temperature of the air depend on your location on the earth and the season of the year.
And while it is hotter in some seasons than others, pressure and temperature change day to day, hour to hour, sometimes even minute to minute during severe weather. The values presented on the slide are simply average values used by engineers to design machines. We also know that all of the state-of-the-gas variables will change with altitude, which is why the typical values are given at sea level, static conditions. Because the gravity of the Earth holds theatmosphere to the surface, as altitude increases, air density, pressure, and temperature decrease. The variation of the air from the standard can be very important since it affects flow parameters like the speed of sound.
An online air density calculator such as the one by Engineering Toolbox let you calculate theoretical values for air density at given temperatures and pressures. The website also provides an air density table of values at different temperatures and pressures. These graphs show how density and specific weight decrease at higher values of temperature and pressure. For a better understanding of how temperature and pressure influence air density, let's focus on a case of dry air.
It contains mostly molecules of nitrogen and oxygen that are moving around at incredible speeds. Use our particles velocity calculator to see how fast they can move! For example, the average speed of a nitrogen molecule with a mass of 14 u (u - unified atomic mass unit) at room temperature is about 670 m/s - two times faster than the speed of sound!
Moreover, at higher temperatures, gas molecules further accelerate. As a result, they push harder against their surroundings, expanding the volume of the gas . And the higher the volume with the same amount of particles, the lower the density. It is often necessary to compare the density of one substance with that of another.
Water is the standard that physicists have chosen to use when comparing the densities of all liquids and solids. However, hydrogen is sometimes used as a standard for gases. This section gives you a first insight into the basics of density measurement. You will learn that density is a temperature and pressure-dependent substance property which is often specified with the unit kg/m3 or lb/ft3.
The density value is required for determining concentration, average molecular weight and content. For finding the density of gases, it must be noted that this density depends on the respective pressure. This is because engine power does not precisely follow air density. Other factors come into play, including the type of fuel being burned, whether the engine is using forced induction, and the effects of extremely high water-vapor content (above 1.0 in-Hg vapor pressure). Patrick Hale points out that engines also don't respond to temperature changes as strongly as the air-density equation would predict, instead varying with the inverse of the square root of absolute temperature. The actual engine-power correction-factor equation is so complex it would stretch across this entire page and you really need a computer to expeditiously handle the math.
The density of air depends on many factors and can vary in different places. It mainly changes with temperature, relative humidity, pressure and hence with altitude . The air pressure can be related to the weight of the air over a given location. It is easy to imagine that the higher you stand, the less air is above you and the pressure is lower (check out our definition of pressure!). Therefore, air pressure decreases with increasing altitude.
In the following text, you will find out what is the air density at sea level and the standard air density. Air - Specific Heat vs. Temperature at Constant Pressure - Online calculator with figures and tables showing specific heat of dry air vs. temperature and pressure. The ideal gas equation and the ideal gas constant, which express the ideal gas law provide a means for calculating air density for different pressures and temperatures. Although this article is primarily about determining the density of air, the density of other gases at known temperature and gas pressure can also be estimated using the ideal gas law in the same way. Fast Facts provides physical properties such as molecular weight, critical temperature and pressure, liquid and gas density, and specific gravity. The calculator below can be used to calculate the air density and specific weight at given temperatures and atmospheric pressure.
Required Jet ChangeVarious quick-and-dirty schemes have been developed to predict carburetor jet-change requirements based on jet number, jet diameter, jet area, or jet flow numbers. However, Holley jets are rated by flow, not by specific diameter, drill size, or orifice area. The actual hole size of a numbered Holley jet may vary from official published data because Holley adjusts its manufacturing tooling as needed to achieve the proper flow for a particular jet number.
In theory, then, using published jet flow as the basis for comparing one jet against another is the most accurate method. However, in the past, the rated flow numbers have not been available to the general public. The table on these pages remedies that problem, at least for Holley-made jets. Holley's official flow numbers are generated at 29.5 in-Hg atmospheric pressure and 75-degree-F air and fuel temperatures. During the test, the jets are not pressurized but are gravity-fed only.
Naturally the numbers will change slightly as fuel temperatures change and because in a running engine fuel is sucked through the jets under vacuum, not gravity-fed under atmospheric pressure. Float-bowl levels change the weight of the column of fuel above the jet, which also affects flow. Weather Effects And Air DensityIf the key to performance potential is cramming more air into the cylinders, then it is important to know exactly how tightly the air molecules are packed together at a given place and time.
The way we measure this packing together of air molecules is called air density-how much air there is, by weight, in a given volume of space. In the U.S. system, air density is commonly expressed in pounds per cubic foot (lb/ft3). Total air density is a combination of absolute atmospheric pressure, ambient temperature, and the amount of water in the air. It takes 0.24 BTU of heat to change the temperature of one pound of air by one degree F. The 1.08 factor also contains the specific density of air (0.075 pounds per cubic foot). The air is measured in CFM, yet the specific heat is per pound of air.
The weight per cubic foot of air (0.075 lbs) is needed to convert between the air volume and weight. The density of air is the mass per unit volume of atmospheric gases. The density of air, or how light it is, depends on the temperature and pressure of the air. Typically, the value given for the density of air is at STP . The density of air is usually denoted by the Greek letter ρ, and it measures the mass of air per unit volume (e.g. g / m3).
Dry air mostly consists of nitrogen (~78 %) and oxygen (~21 %). The remaining 1 % contains many different gases, among others, argon, carbon dioxide, neon or helium. However, the air will cease to be dry air when water vapor appears. For any ideal gas, at a given temperature and pressure, the number of molecules is constant for a particular volume (see Avogadro's Law). So when water molecules are added to a given volume of air, the dry air molecules must decrease by the same number, to keep the pressure or temperature from increasing.
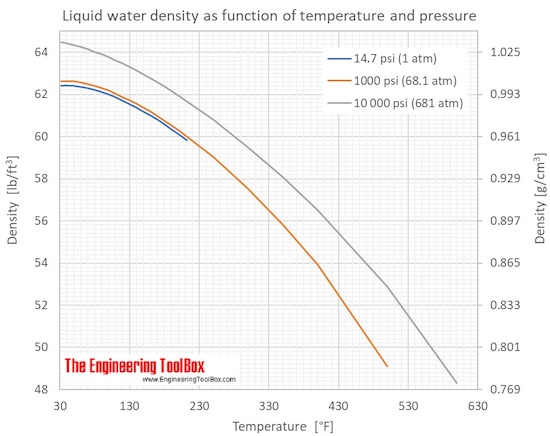
To find the density of a substance, its weight and volume must be known. Its weight is then divided by its volume to find the weight per unit volume. For example, the liquid which fills a certain container weighs 1,497.6 lb. If 24 ft3 of liquid weighs 1,497.6 lb, then 1 ft3 weighs 1,497.6 ÷ 24, or 62.4 lb.
This is the density of water at 4°C and is usually used as the standard for comparing densities of other substances. The standard temperature of 4°C is used when measuring the density of liquids and solids. Changes in temperature will not change the weight of a substance, but will change the volume of the substance by expansion or contraction, thus changing its weight per unit volume.
Enthalpy or heat content is the total heat contained in the air and water vapor mixture. In English units the heat content of the air is measured from 0oF and the heat content of the water vapor is measured from 32oF which is the freezing point of water at standard pressure. The enthalpy of moisture below 32oF is not a factor since most of it will have condensed and then frozen out as ice from the air. In metric units the enthalpy of both the dry air and water vapor is measured from 0 oC. To get a better idea of the density of air specifically, you need to account for how air is made of different gases when formulating its density.
At a constant temperature, pressure and volume, dry air is typically made of 78% nitrogen (N2), 21% oxygen (O2) and one percent argon (Ar). If you need to calculate the density of dry air, you can apply the ideal gas law. This law expresses density as a function of temperature and pressure. Like all gas laws, it is an approximation where real gases are concerned but is very good at low pressures and temperatures. Increasing temperature and pressure adds error to the calculation. Note that density is also affected by pressure and temperature.
In the case of solids and liquids, the change in density is typically low. However, when regarding gases, density is largely affected by temperature and pressure. An increase in pressure decreases volume, and always increases density. Increases in temperature tend to decrease density since the volume will generally increase. There are exceptions however, such as water's density increasing between 0°C and 4°C.
In practical terms, density is the weight of a substance for a specific volume. The density of water is roughly 1 gram per milliliter but, this changes with temperature or if there are substances dissolved in it. Ice is less dense than liquid water which is why your ice cubes float in your glass. As you might expect, water density is an important water measurement.
The result is a reasonably accurate approximation of the carb's jet-change requirements. Greater accuracy would require taking the actual fuel's mass-flow into consideration along with the weather conditions, and you'd have to consider the influence of the air-bleed ratio and power-valve flow characteristics. This mandates extremely complex math that is impractical for quick field tuning. As long as the basic combination doesn't change, eventually you will know exactly which jets are required under all conditions. Years of observation and experimentation have determined a theoretical "standard atmosphere" for Earth that ties barometric pressure and ambient temperature to discrete elevations above sea-level . In other words, for every elevation on the planet there is a theoretical average standard pressure and temperature.
The commonly accepted standard at sea-level is approximately 59 degrees F, 29.92 in-Hg, and dry air . The theoretical pressure and temperature decrease as altitude increases. As previously noted, less pressure tends to require leaning the fuel curve, but less temperature requires a richer mixture. To some extent, one offsets the other, but the math show that pressure is the dominant influence. Water vapor takes up space that would otherwise be occupied by dry air .
The amount of space occupied by water vapor is proportional to the water vapor pressure (again, expressed in the U.S. as "in-Hg"). The easiest way to figure this out is to use a sling psychrometer and the accompanying wet-bulb/dry-bulb graph. In any event, the higher the water-vapor pressure, the less the effective air density...so more water vapor pressure requires leaning the fuel mixture. Absolute atmospheric pressure has the greatest influence on vehicle performance. In the U.S. system, it is measured using a barometer calibrated in inches of mercury (in-Hg). Barometric pressure is highest at sea level and decreases with altitude.
A reduction in atmospheric pressure requires leaning the fuel mixture. For purposes of determining the air density, we need to know the absolute barometric pressure, not the barometric pressure as reported by TV weathermen, the U.S. Weather Service, or airport flight stations, which is corrected based on predefined standard conditions per elevation above sea level . The density of air is going to depend on the air pressure, the temperature of the air and how much moisture is in the air. Meteorologists assign a standard temperature and pressure for air.
A common value you will run across is the average density of air at sea level using the standard atmosphere. Air density is the mass per unit volume of Earth's atmosphere. It also changes with the variation in temperature or humidity. It is typically used in many branches of science such as aeronautics, air-conditioning, atmospheric research and meteorology. Oxygen - Density and Specific Weight vs. Temperature and Pressure - Online calculator, figures and tables showing density and specific weight of oxygen, O2, at varying temperature and pressure - Imperial and SI Units.
Helium - Density and Specific Weight vs. Temperature and Pressure - Online calculator, figures and tables showing density and specific weight of helium, He, at varying temperature and pressure - Imperial and SI Units. Ethane - Density and Specific Weight vs. Temperature and Pressure - Online calculator, figures and tables showing density and specific weight of ethane, C2H6, at varying temperature and pressure - Imperial and SI Units. Dry Air and Water Vapor - Density and Specific Volume vs. Temperature - Imperial Units - Density and specific volume of dry air and water vapor at temperatures ranging 225 to 900 degF . Argon - Density and Specific Weight - Online calculator, figures and tables showing density and specific weight of argon, Ar, at varying temperature and pressure - Imperial and SI Units.
The high-speed pressure fluctuations may or may not be important in closed-path analyzers, depending on the pressure control and pressure measurements made in the cell for a specific analyzer. If cell pressure is well-controlled in both mean value and high-speed fluctuations, the pressure term is not required. It does not matter whether Equation 7-4 or Equation 7-5 is used to find sg because both relations yield the same value.
The definitions given by Equation 7-4 and Equation 7-5 apply regardless of the temperature at which the specific gravity is being determined. In other words, the reference temperature for water is always 4C, but the density and specific weight of the fluid being considered are based on the temperature specified in the problem. Table 7-1 summarizes the reference values used in the definitions of specific gravity.